How Do You Know the Minimum and Maximum of a Function
10
MAXIMUM AND MINIMUM
VALUES
The turning points of a graph
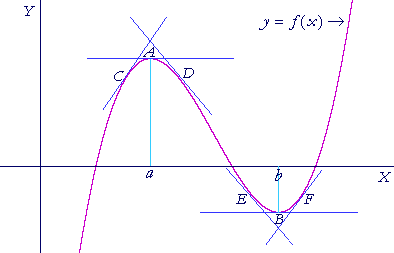
W Eastward SAY THAT A FUNCTION f(x) has a relative maximum value at x = a,
if f(a) is greater than any value immediately preceding or follwing.
We call it a "relative" maximum because other values of the function may in fact be greater.
We say that a office f(x) has a relative minimum value at 10 = b,
if f(b) is less than any value immediately preceding or follwing.
Once again, other values of the function may in fact be less. With that agreement, so, we will drop the term relative.
The value of the function, the value of y, at either a maximum or a minimum is called an extreme value.
Now, what characterizes the graph at an extreme value?

The tangent to the curve is horizontal. We see this at the points A and B. The slope of each tangent line -- the derivative when evaluated at a or b -- is 0.
f '(x) = 0.
Moreover, at points immediately to the left of a maximum -- at a pointC -- the gradient of the tangent is positive:f '(ten) > 0. While at points immediately to the correct -- at a point D -- the slope is negative:f '(x) < 0.
In other words, at a maximum, f '(x) changes sign from + to − .
At a minimum, f '(ten) changes sign from − to + . We tin run into that at the points E and F.
We can also observe that at a maximum, at A, the graph is concave downwardly. (Topic 14 of Precalculus.) While at a minimum, at B, information technology is concave upward.
A value of x at which the function has either a maximum or a minimum is called a critical value. In the figure --

-- the disquisitional values are x =a and 10 =b.
The disquisitional values determine turning points, at which the tangent is parallel to the x-centrality. The disquisitional values -- if any -- will be the solutions tof '(x) = 0.
Example 1. Allowf(x) = 10 ii − 6x + v.
Are there any critical values -- any turning points? If so, do they decide a maximum or a minimum? And what are the coördinates on the graph of that maximum or minimum?
Solution.f '(x) = 2x − 6 = 0 impliesx = three. (Lesson 9 of Algebra.)
x = three is the only disquisitional value. It is the ten-coördinate of the turning point. To decide the y-coördinate, evaluate f at that critical value -- evaluate f(three):
| f(x) | = | x two − 6x + v |
| f(3) | = | 32 − vi· iii + 5 |
| = | −iv. | |
The farthermost value is −4. To see whether it is a maximum or a minimum, in this instance we can just expect at the graph.
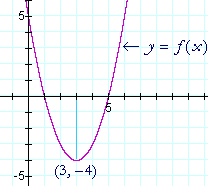
f(ten) is a parabola, and we tin see that the turning point is a minimum.
By finding the value of x where the derivative is 0, then, we accept discovered that the vertex of the parabola is at (3, −4).
Just we will not always be able to look at the graph. The algebraic condition for a minimum is that f '(10) changes sign from − to + . We come across this at the points E, B, F to a higher place. The value of the gradient is increasing.
Now to say that the slope is increasing, is to say that, at a disquisitional value, the 2nd derivative (Lesson 9) -- which is charge per unit of modify of the slope -- is positive.
Again, here isf(x):
| f(x) | = | x 2 − vix + 5. |
| f '(x) | = | 2x − half-dozen. |
| f ''(x) | = | 2. |
f '' evaluated at the critical value 3 -- f''(three) = 2 -- is positive. This tells us algebraically that the critical value iii determines a minimum.
Sufficient weather

We tin can now state these sufficient conditions for extreme values of a function at a critical value a:
The function has a minimum value at x =a if f '(a) = 0
and f ''(a) = a positive number.
The function has a maximum value at x =a if f '(a) = 0
and f ''(a) = a negative number.
In the case of the maximum, the slope of the tangent is decreasing -- it is going from positive to negative. Nosotros tin come across that at the points C, A, D.
Example two. Permitf(10) = 210 3− ixx ii + 12x − 3.
Are at that place whatever extreme values? First, are at that place any critical values -- solutions to f '(ten) = 0 -- and practice they decide a maximum or a minimum? And what are the coördinates on the graph of that maximum or minimum? Where are the turning points?
| Solution.f '(x) = 6ten 2 − xviiix + 12 | = | half-dozen(x two − threeten + 2) |
| = | 6(x − 1)(10 − 2) | |
| = | 0 | |
implies:
x = 1 orten = 2.
(Lesson 37 of Algebra.)
Those are the critical values. Does each one determine a maximum or does it determine a minimum? To answer, we must evaluate the second derivative at each value.
| f '(x) | = | 6ten 2 − 18ten + 12. |
| f ''(ten) | = | 12x − 18. |
| f ''(i) | = | 12 − 18 = −6. |
The second derivative is negative. The part therefore has a maximum at x = 1.
To detect the y-coördinate -- the extreme value -- at that maximum nosotros evaluatef(1):
| f(ten) | = | iiten 3− 9ten 2 + 12x − 3 |
| f(1) | = | 2 − 9 + 12 − 3 |
| = | ii. | |
The maximum occurs at the bespeak (i, two).
Adjacent, does ten = two make up one's mind a maximum or a minimum?
| f ''(x) | = | 12x − 18. |
| f ''(2) | = | 24 − xviii = 6. |
The second derivative is positive. The role therefore has a minimum at x = 2.
To find the y-coördinate -- the extreme value -- at that minimum, we evaluate f(2):
| f(ten) | = | 210 3 − 910 two + 12x − three. |
| f(ii) | = | 16 − 36 + 24 − 3 |
| = | 1. | |
The minimum occurs at the bespeak (two, 1).
Here in fact is the graph off(x):
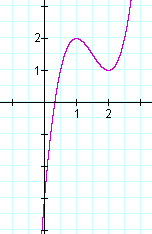
Solutions to f ''(x) = 0 indicate a point of inflection at those solutions, non a maximum or minimum. An case is y =ten three.y'' = 6x = 0 implies x = 0. But x = 0 is a point of inflection in the graph of y =x 3, non a maximum or minimum.
Another example is y = sin x. The solutions to y'' = 0 are the multiplies of π, which are points of inflection.
Problem i. Find the coördinates of the vertex of the parabola,
y = ten 2 − 8x + one.
To meet the answer, pass your mouse over the colored area.
To cover the reply again, click "Refresh" ("Reload").
Do the trouble yourself first!
y' = 2x − 8 = 0.
That implies x = 4. That's the x-coördinate of the vertex. To find the y-coördinate, evaluate y at 10 = 4:
y = 42 − 8· 4 + 1 = −15.
The vertex is at (4, −15).
Problem 2. Examine each role for maxima and minima.
a) y = ten 3 − 310 2 + 2.
y' = 3x 2 − 610 = iiix(x − 2) = 0 implies
10 = 0 or x = 2.
y''(10) = 6x − 6.
y''(0) = −6.
The 2d derivative is negative. That ways there is a maximum at 10 = 0. That maximum value is
y(0) = ii.
Adjacent,
y''(2) = 12 − 6 = 6.
The 2nd derivative is positive. That means there is a minimum at x = two. That minimum value is
y(ii) = 23 − 3· 22 + 2 = 8 − 12 + ii = −two.
b) y = −twox iii − 3x 2 + 12 x + 10.
At x = 1 there is a maximum of y = 17.
At x = −two there is a minimum of y = −10.
c) y = 2x 3 + 3x 2 + 12 x − 4.
Since f '(x) = 0 has no real solutions, in that location are no extreme values.
d) y = iii10 four− 4ten 3 − 12x 2 + 2.
At ten = 0 there is a maximum of y = 2.
At ten = −1 in that location is a minimum of y = −3.
At x = 2 there is a minimum of y = −30.
![]()
Next Lesson: Applications of maximum and minimum values
Table of Contents | Habitation
Please brand a donation to keep TheMathPage online.
Fifty-fifty $1 will aid.
Copyright © 2021 Lawrence Spector
Questions or comments?
Eastward-mail: teacher@themathpage.com
Source: https://themathpage.com/aCalc/max.htm
0 Response to "How Do You Know the Minimum and Maximum of a Function"
Post a Comment